Derivadas e integrales
|
|
|
- Susana Sandoval Gómez
- hace 7 años
- Vistas:
Transcripción
1 Derivadas e integrales Álvarez S., Caballero M.V. y Sánchez M a M salvarez@um.es, m.victori@um.es, marvega@um.es
2 ÍNDICE Matemáticas Cero Índice. Definiciones 3. Herramientas 4.. Reglas de derivación Crecimiento y extremos Representación gráfica Cálculo de primitivas Cálculo de áreas Ejercicios resueltos 9 4. Ejercicios propuestos 30
3 . Definiciones Derivada de una función: Sea la función f(x), si el límite siguiente existe f y (x 0 ) = lím x 0 x = lím f(x 0 + x) f(x 0 ) x 0 x = lím x x0 f(x) f(x 0 ) x x 0 se dice que la función es derivable en x 0 y f (x 0 ) es el valor de la derivada de f en el punto x 0. Recta tangente: Sea y = f(x) una función derivable en x 0 Dom(f), la recta tangente a la función en el punto x 0, es la recta que pasa por el punto (x 0, f(x 0 )) y cuya pendiente es f (x 0 ). Punto crítico: Sea y = f(x) una función derivable en x 0 Dom(f). Se dice que x 0 es un punto crítico de f cuando f (x 0 ) = 0. Máximo relativo: Una función y = f(x) tiene un máximo relativo o local en x 0 cuando para puntos x próximos a x 0 se verifica que f(x) f(x 0 ). Mínimo relativo: Una función y = f(x) tiene un mínimo relativo o local en x 0 cuando para puntos x próximos a x 0 se verifica que f(x) f(x 0 ). Extremo relativo: Es un máximo o un mínimo relativo. Máximo absoluto: Una función y = f(x) tiene un máximo absoluto (o global) en x 0 cuando para cualquier x Dom(f) se verifica que f(x) f(x 0 ). Mínimo absoluto: Una función y = f(x) tiene un mínimo absoluto (o global) en x 0 cuando para cualquier x Dom(f) se verifica que f(x) f(x 0 ). Primitiva de una función: F (x) es una primitiva de una función continua f(x) si F (x) = f(x). Integral indefinida: La integral indefinida de una función continua f(x) es el conjunto de todas sus primitivas. Si F (x) es una primitiva de f(x), la integral indefinida de f(x) se escribe f(x)dx = F (x) + cte. 3
4 Integral definida: Si f(x) es una función continua en un intervalo [a, b] y F (x) una primitiva cualquiera de f(x), la integral definida de f(x) entre a y b es el número real b. Herramientas.. Reglas de derivación a f(x)dx = F (b) F (a) (Regla de Barrow).. Derivada de la función constante: y = f(x) = K = y = f (x) = 0.. Derivada de la función potencia: y = f(x) = x n, n R = y = f (x) = nx n. 3. Derivada de la función logaritmo: y = ln x = y = f (x) = x. 4. Derivada de la función exponencial: y = e x = y = f (x) = e x. 5. Si f(x) es una función derivable, entonces la función y = λf(x) es derivable y su derivada vale y = λf (x). 6. Derivada de la suma: Si f(x) y g(x) son funciones derivables, entonces (f + g)(x) es derivable y (f + g) (x) = f (x) + g (x). Ejemplo. Hallar la función derivada de la función f(x) = x +. La función derivada es f (x) =, pues f(x) = g(x)+h(x), con g(x) = x y h(x) =.Y como la derivada de una suma es la suma de las correspondientes derivadas, f (x) = g (x) + h (x), con g (x) = y h (x) = Derivada del producto: Si f(x) y g(x) son funciones derivables, entonces (fg)(x) es derivable y (fg) (x) = f (x)g(x) + f(x)g (x). Ejemplo. Hallar la función derivada de la función f(x) = (x + )e x. 4
5 . Reglas de derivación Matemáticas Cero f (x) = () (x + ) e x + (x + )(e x ) = () e x + (x + )e x = e x (x + 3). La igualdad () resulta de utilizar la regla de derivación de un producto, y la igualdad () se obtiene simplemente sustituyendo el valor de las derivadas ( que se conocen por las reglas de derivación). 8. Derivada del cociente: Si f(x) y g(x) son funciones derivables, entonces (f/g)(x) es derivable cuando g(x) 0, y ( ) f (x) = f (x)g(x) f(x)g (x). g (g(x)) Ejemplo.3 Hallar la función derivada de la función f(x) = 5x e. x f (x) = () (5x) e x 5x (e x ) = 5 ex 5x e x 5( x) =, donde la (e x ) e x e x igualdad () resulta de aplicar la regla de derivación de un cociente. 9. Regla de la cadena: Sean f(x) y g(x) funciones derivables, entonces (g f) (x) = g (f(x))f (x). Como consecuencia de la regla de la cadena, se obtiene que: a) Derivada de la potencia de una función: y = (f(x)) n, n R = y = n(f(x)) n f (x). b) Derivada del logaritmo de una función: y = ln f(x) = y = f (x) f(x). c) Derivada de la exponencial de una función: y = e f(x) = y = f (x)e f(x). Ejemplo.4 Hallar la función derivada de las siguientes funciones: f(x) = (x 0) 7. g(x) = ln(x + 4). h(x) = e x3. f (x) = () 7(x 0) 6 (x 0) = 7(x 0) 6 (x), donde la igualdad () resulta de aplicar la regla de derivación de la potencia de una función ( la función (x 0) en este caso). 5
6 . Crecimiento y extremos Matemáticas Cero g (x) = () (x + 4) x + 4 = x, correspondiendo la igualdad () a x + 4 la derivada del logaritmo de una función. h (x) = (3) (x 3 ) e x3 = 3x e x3, la igualdad (3) corresponde a la derivada de la exponencial de una función... Crecimiento y extremos Condición de crecimiento o decrecimiento Sea f(x) una función derivable en x 0, se cumple que: a) Si f (x 0 ) > 0, entonces f(x) es creciente en x 0. b) Si f (x 0 ) < 0, entonces f(x) es decreciente en x 0. c) Si f (x 0 ) = 0 caso dudoso. Condición de primer orden de extremo relativo Sea una función y = f(x) derivable en x 0. Si f(x) tiene un extremo relativo en x 0, entonces f (x 0 ) = 0. Condición de segundo orden de extremo relativo Sea x 0 un punto crítico de una función y = f(x) dos veces derivable. Entonces: Si f (x 0 ) < 0, entonces en x 0 la función tiene un máximo relativo. Si f (x 0 ) > 0, entonces en x 0 la función tiene un mínimo relativo. Otro método Sea x 0 un punto crítico de una función derivable y = f(x). Entonces:. Si f (x) > 0 para puntos x próximos a x 0, x < x 0 (por la izquierda) y f (x) < 0 en puntos x próximos a x 0, x > x 0 (por la derecha), entonces f(x) tiene un máximo relativo en x 0.. Si f (x) < 0 para puntos x próximos a x 0, x < x 0 (por la izquierda) y f (x) > 0 en puntos x próximos a x 0, x > x 0 (por la derecha), entonces f(x) tiene un mínimo relativo en x Si f (x) tiene el mismo signo para puntos x próximos a x 0,entonces f(x) no tiene un extremo relativo en x 0. 6
7 .3 Representación gráfica Matemáticas Cero.3. Representación gráfica La representación gráfica de una función real y = f(x) requiere:. Determinar el dominio donde la función está definida.. Identificar los puntos de corte con los ejes coordenados. 3. Estudiar la existencia de asíntotas (su definición se da en el tema de límites y continuidad de funciones). 4. Estudiar la existencia de puntos de corte con las asíntotas: las curvas y = f(x) no cortan a las asíntotas paralelas a OY; pero sí pueden cortar a las asíntotas horizontales y oblicuas. 5. Identificar los intervalos de crecimiento y decrecimiento. 6. Determinar (si existen) los máximos y los mínimos relativos..4. Cálculo de primitivas INTEGRALES INMEDIATAS x n dx = xn+ + K si n n + dx = ln(x) + K x e x dx = e x + K Propiedades. Dadas dos funciones f y g : [f(x) + g(x)] dx = f(x)dx + g(x)dx. Ejemplo.5 Calcular (x 3 + e x )dx. (x 3 + e x )dx = x 3 dx + e x dx = 4 x4 + e x + K.. Dada una función f y λ una constante: λf(x)dx = λ f(x)dx. 7
8 .5 Cálculo de áreas Matemáticas Cero 3. Cambio de variable en una integral indefinida: f(g(x))g (x)dx = f(t)dt siendo t = g(x). Ejemplo.6 Calcular 5 7x + dx. Mediante el cambio de variable t = 7x +, se tiene que dt = 7dx, y la integral se reescribe en términos de t como 7 t/5 dt, y 7 t/5 dt = t /5 dt = t6/5 + K = 5 4 (7x + )6/5 + K. Ejemplo.7 Deducir que para toda función derivable f(x), se cumple que: a) f(x) n f (x)dx = f(x)n+ + K si n. n + b) f (x) dx = ln(f(x)) + K. f(x) c) e f(x) f (x)dx = e f(x) + K. a) Mediante el cambio de variable t = f(x), se tiene que dt = f (x)dx, y la integral se reescribe como f(x) n f (x)dx = t n dt, que es inmediata y vale tn+ n + + K. Al deshacer el cambio, queda f(x)n+ n + + K. b) Igual que antes, con el cambio de variable t = f(x), se tiene que dt = f (x)dx, y la integral se reescribe como f (x) f(x) dx = t dt, que es inmediata y vale ln t + K = ln(f(x)) + K. c) Con el mismo cambio que en los anteriores apartados, t = f(x), e f(x) f (x)dx = e t dt = e t + K = e f(x) + K..5. Cálculo de áreas El área bajo una curva y = f(x) y sobre el intervalo [a, b] (para f(x) 0 si x [a, b]) es b a f(x)dx = F (b) F (a) con F (x) una primitiva cualquiera de f(x) 8
9 Si la función no fuese positiva en el intervalo, el área limitada por la curva el eje de abscisas y las recta x = a y x = b es b a f(x)dx = F (b) + F (a). Si c [a, b], se cumple b a f(x)dx = c 3. Ejercicios resueltos a f(x)dx + b c f(x)dx. Ejercicio Hallar las funciones derivadas de las siguientes funciones: a) f(x) = x 4. b) f(x) = 5x 3. c) f(x) = 5x. d) f(x) = 5 x + 3 x 7 x. e) f(x) = x 4 + 5x 3 + 3x 5 x. f) f(x) = x ln x. g) f(x) = (x 4 x 3 )e x. h) f(x) = x4 + x ln x. i) f(x) = e x3 5x. j) f(x) = (3x ) e x3 +7x. k) f(x) = l) f(x) = ln x 3x + 5. ( ) 5x +. 3x 9
10 a) f (x) = 4x 3. b) f (x) = 5 (x 3 ) = 5 3x = 5x, ya que la derivada de un número por una función es el número por la derivada de la función, y la derivada de x 3 es 3x. c) f (x) = 5, ya que 5x f (x) = ( 5x ) = [ (5x ) /] = (5x ) / 5, donde se ha utilizado la derivada de la potencia de una función, pues y = 5x = (5x ) /. d) f (x) = 5x 5 x + 3x 3 x + 7x 7 x, que se obtiene escribiendo f(x) como f(x) = x /5 + (x) /3 x /7, con lo que f (x) = (x /5 ) + ( (x) /3) (x /7 ) = 5x x/5 + 3x (x)/3 + 7x x /7, donde las derivadas de los distintos sumandos resultan de aplicar la derivada de la función potencia. e) f (x) = 4x 3 + 5x + 6x 5, lo que resulta de sumar las derivadas de x los distintos sumandos, que a su vez se calculan en la forma indicada en los anteriores apartados. f) Aplicando la regla de derivación de un producto, f (x) = x ln x + x(ln x) = ln x + x x = ln x +. g) Por la regla de derivación de un producto, f (x) = (x 4 x 3 ) e x + (x 4 x 3 )(e x ) = (4x 3 6x)e x + (x 4 x 3 )e x = e x (x 4 + 4x 3 6x). h) Aplicando la regla de derivación de un cociente, f (x) = (x4 + x ) ln x (x 4 + x )(ln x) (ln x) = 0
11 (4x 3 + x) ln x (x 4 + x )(/x) (ln x) = (4x 3 + x) ln x x 3 x (ln x). i) La función que hay que derivar es de la forma e h(x) = (g h)(x) siendo g(x) = e x y h(x) = x 3 5x, y por la regla de la cadena, f (x) = ( e h(x) ) = (g h) (x) = g (h(x)) h (x) = e h(x) h (x). Luego, f (x) = e x3 5x (x 3 5x) = e x3 5x (3x 5). j) Utilizando la regla de derivación de un producto y expresión la derivada de la función exponencial obtenida en i), f (x) = (3x ) e x3 +7x + (3x ) (e x3 +7x ) = 6xe x3 +7x + (3x ) e x3 +7x (3x + 7) = e x3 +7x (6x + (3x ) (3x + 7)). k) f (x) = (x ) ( 3x + 5) (x )( 3x + 5) ( 3x + 5) = (x) 3x + 5 (x ) 3 x ( 3x + 5) = ( ( 3 3 x+5) ) 3 3x + 5. ( ) 5x + 8 l) f 3x (3x ) 8 (x) = ( ) = ( ) = 5x + 5x + (3x ) (5x + ). 3x 3x ( ) 5x + Alternativamente se puede escribir f(x) = ln = ln(5x + ) 3x ln(3x ), con lo que f (x) = 5 5x + 3 3x = 8 (3x ) (5x + ). Ejercicio Calcular las derivadas de las siguientes funciones en los puntos indicados: a) f(x) = 3 x3 x + 3x, en x = y x = 0.
12 b) g(x) = e 5x 4 ln x, en x = y x =. c) h(x) = ln(x x), en x = y x =. x a) f (x) = x x + 3, luego f () = 4 y f (0) = 3. b) g (x) = 5e 5x 8 x, con lo que g ( ) = 5e5/ 6 y g () = 5e 5 8. c) h (x) = x ln (x x) 4x x x x, luego h ( ) = ln 3 + 5/3 y h () = 3. Ejercicio 3 Para las funciones siguientes, estudiar su crecimiento y sus extremos relativos: a) f(x) = x x + 5. b) f(x) = 3 x3 x 4x +. c) f(x) = x x 3. a) Sea f(x) = x x + 5, su dominio es R, y es continua y derivable en su dominio. La función derivada es f (x) = x. Para obtener los puntos críticos se resuelve la ecuación f (x) = x = 0, cuya única solución es x = /. Por tanto, la función solo tiene un punto crítico en x = /. Para estudiar el crecimiento y el decreciomiento se analiza el signo de f (x). Es fácil obtener que f (x) > 0 para x (/, + ) y f (x) < 0 para x (, /). Por tanto, f(x) es creciente en (/, + ) y decreciente en (, /).
13 Como se ha obtenido que f(x) es creciente en (/, + ) y decreciente en (, /), se puede utilizar la correspondiente propiedad que permite afirmar que en x = /, la función tiene un mínimo relativo. b) Sea f(x) = 3 x3 3 x 4x +, su dominio es R, y es continua y derivable en su dominio. Para obtener los puntos críticos se resuelve la ecuación f (x) = x 3x 4 = 0, cuyas soluciones son x = y x = 4. Escribiendo ahora f (x) como f (x) = (x + )(x 4), se observa que f (x) > 0 ( y por tanto f es creciente) para x (, ) (4, + ) y f (x) < 0 ( f decreciente) para x (, 4). El comportamiento de crecimiento y decrecimiento de la función indica que en x =, la función tiene un máximo relativo y tiene un mínimo relativo en x = 4. c) Sea f(x) = x x 3. Su dominio es R {0}, donde es continua y derivable. f (x) = x + 3 x 4. La función derivada se anula en x = 3 y x = 3. Por tanto, éstos son los puntos críticos de la función. Escribiendo ahora f (x) como f (x) = (x 3)(x + 3), se observa que f (x) < 0 ( y por tanto f es decreciente) para x (, 3) ( 3, + ) y f (x) > 0 ( f creciente) para x ( 3, 0) (0, 3). Esto permite afirmar que la función tiene un mínimo relativo en x = 3 y un máximo relativo en x = 3. Ejercicio 4 Calcular los extremos relativos de la función f(x) = x (x 3). x 4 3
14 La función derivada es f (x) = 3x 6x. 3x 6x = 0 x = 0 o x =. Por tanto, los posibles extremos relativos son x = 0 y x =. La confirmación o no de extremos relativos en x = 0 y x =, se puede hacer observando el signo de la derivada. f (x) > 0 si x (, 0) (, + ) y f (x) < 0 si x (0, ). Luego, f es creciente en (, 0) (, + ) y decreciente en (0, ). Esto indica que en x = 0, hay un máximo relativo y en mínimo relativo. x = un O bien se calcula la derivada segunda, f (x) = 6x 6, obteniéndose que f (0) < 0 y f () > 0. El comportamiento en cuanto al crecimiento indica también que en x = tiene un mínimo absoluto y no tiene máximos absolutos. Ejercicio 5 Dada la función f(x) = Dominio. Máximos y mínimos. Intervalos de crecimiento. Asíntotas. 3x x +, determinar: La función es una fracción, y se puede calcular la imagen de cualquier número real puesto que ningún número real anula el denominador. Por tanto, Dom(f) = R. Puntos críticos: f (x) = 6x (x + ) = 0 x =. Entonces: 4
15 Si x (, 0), f (x) < 0, por tanto, f(x) decrece. Si x (0, +, 0), f (x) > 0, luego f(x) crece. Por tanto, la función tiene en x = 0 un mínimo relativo de valor f(0) = 0. No tiene asíntotas verticales. Asíntotas horizontales lím x ± 3x x + = 3 La recta y = 3 es una asíntota horizontal de la función. Ejercicio 6 Hacer la representación gráfica de la función f(x) = x x+. Dom(f) = R puesto que la función es un polinomio. No tiene asíntotas verticales. No tiene asíntotas horizontales, pues: lím x x x + = + lím x + x x + = +. Al no tener asíntotas horizontales, puede tener asíntotas oblicuas. Asíntotas oblicuas: x x + m = lím x ± x Por tanto, no tiene asíntotas oblicuas. Puntos críticos, crecimiento y extremos =. f (x) = x x =. Si x (, ), f (x) < 0, por tanto f(x) crece. Si x (, + ), f (x) > 0, entonces f(x) crece. Luego, en x = la función tiene un mínimo relativo de valor f() = 0. La representación gráfica se da en la figura. Ejercicio 7 Hacer la representación gráfica de la función f(x) = 5 x3 x.
16 Figura : Representación gráfica de la función del ejercicio 6 Dom(f) = R {, }, puesto que x = 0 x =, x =. Asíntotas verticales: x 3 lím x x = + lím x 3 x + x =. La recta x = es una asíntota vertical de la función. x 3 lím x x = lím x 3 x + x = +. La recta x = es una asíntota vertical de la función. Asíntotas horizontales: lím x x 3 x = lím x + x 3 x = +. La función no tiene asíntotas horizontales, puede tener asíntotas oblicuas. Asíntotas oblicuas: m = lím x ± x 3 x(x ) = n = lím x ± La recta y = x es asíntota oblicua de la función. 6 x 3 x x = 0.
17 Puntos críticos, crecimiento y extremos f (x) = x (x 3) (x ) = 0 x = 0, x = 3, x = 3. Si x (, 3), f (x) > 0, entonces f(x) crece. Si x ( 3, ), f (x) < 0, entonces f(x) decrece. Si x (, 0), f (x) < 0, por tanto f(x) decrece. Si x (0, ), f (x) < 0, entonces f(x) decrece. Si x (, 3), f (x) < 0, luego f(x) decrece. Si x ( 3, + ), f (x) > 0, con lo que f(x) crece. Por tanto, en x = 3 la función tiene un máximo relativo de valor f( 3) = 3 3 y en x = 3 tiene un mínimo relativo de valor f( 3) = 3 3. La representación gráfica se presenta en la figura. Figura : Representación gráfica de la función del ejercicio 7 Ejercicio 8 Dada la parábola y = x 6x + 0, hallar el punto en el que la recta tangente es paralela al eje de abscisas. La pendiente de la recta tangente a una función en un punto (x 0, f(x 0 )) es el valor de la derivada de la función en el punto x 0, es decir f (x 0 ). Dos rectas son paralelas si tienen la misma pendiente. Por tanto, una recta paralela al eje de abscisas tiene que tener pendiente igual a 0. 7
18 Como y = x 6 = 0 x = 3, el punto buscado es el (3, f(3)) = (3, ). Ejercicio 9 Se divide un alambre de longitud 4 cm en dos partes, de modo que cada una de ellas sea la base de dos rectángulos cuyas alturas sean el triple y el cuádruple de la base considerada respectivamente. Cómo habrá de hacerse la partición para que la suma del área de los rectángulos sea mínima? La base de un rectángulo, se denota como x y su altura 3x. La base del otro rectángulo es y y su altura 4y. La suma x + y = 4. La suma de las áreas de los rectángulos es A = 3x + 4y. Se sustituye y = 4 x y se obtiene la función a minimizar: A(x) = 3x + 4(4 x). A (x) = 4x 336. Por tanto, la función A(x) tendrá un punto crítico cuando x = = 4. Como A (x) = 4 > 0, se trata de un mínimo relativo. Además, si x < 4, A (x) < 0, la función A(x) decrece y si x > 4, como A (x) > 0, A(x) crece. Luego la función A alcanza su menor valor cuando x = 4. La suma de las áreas de los rectángulos será mínima cuando x = 4 e y = 8. Ejercicio 0 Hallar las dimensiones que ha de tener un campo rectangular de superficie 500 m para poder cercarlo con una valla de longitud mínima. La base de un rectángulo, se denota por x y su altura por y. El área del rectángulo es 500 = xy. La longitud de la valla es el perímetro del campo, por tanto P = x+y. Se sustituye y = 500 y se obtiene la función de x a minimizar: x P (x) = x x. 8
19 Puntos críticos: P (x) = 5000 x = 0 x = 50, x = 50. x = 50 no tiene sentido, por tanto se considera solo el punto crítico x = 50. Como P (x) = 0 000, se tiene que P (50) > 0 y en x = 50 hay un x 3 mínimo relativo. Además, si x < 50, P (x) < 0, la función P (x) decrece y si x > 50, como P (x) > 0, P (x) crece. Luego la función P tiene un mínimo absoluto en x = 50. Por tanto, para x = 50 e y = 50, la longitud de la valla es mínima. Ejercicio Realizar las siguientes integrales indefinidas: a) (x 4 4x + 4x )dx. b) ( 3 x + x)dx. c) ( x + x)dx. d) 3x dx. e) e 4x dx. f) 6 x + dx. g) x 3 dx. h) x (x 3 + 4) 4 dx. i) dx (5x ) 3. j) x + 4 dx. (x + 8x) /4 k) ( x + )( x x + )dx. l) (ln x) 4 3x dx. m) e x xdx. 9
20 n) 3x x + dx. ñ) e 5/x x dx. o) x 3 x + x 4 4x + 4x dx. p) x [3 + ln x] 3 dx. q) e x ex + dx. r) x( x + ) dx. s) x(3 + ln x) dx. a) (x 4 4x + 4x )dx = 5 x5 4 3 x3 + x x + K, pues (x 4 4x + 4x )dx = x 4 dx 4x dx + 4xdx dx = x 4 dx 4 x dx + 4 xdx dx = 5 x5 4 3 x3 + x x + K. b) ( 3 x + x)dx = 3 xdx + xdx = x /3 dx + x / dx = x 3 + 3x K. 3 4 c) ( x + x)dx = x dx + xdx. x dx = x dx = ln x + K. xdx = (x) / dx = (x) / dx = 3 (x) 3 +K, ya que (x) / dx = f (x)(f(x)) n dx con f(x) = x y n = /. Una forma alternativa de resolver esta última integral es mediante cambio de variable. Haciendo el cambio de variable t = x, se tiene que dt = dx, y la integral se reescribe en términos de t como t / dt = 3 t 3 + K = 3 (x) 3 + K. 0
21 Luego, ( x + x)dx = ln x + 3 (x) 3 + K. d) 3x dx = 3 3x dx = 3 9 (3x ) 3 + K, ya que 3 3x dx = f (x)(f(x)) n dx con f(x) = 3x y n = /. Alternativamente, mediante cambio de variable t = 3x, se tiene que dt = 3dx, y la integral se reescribe en términos de t como t / dt = 3 9 t 3 + K = 9 (3x ) 3 + K. e) e 4x dx = 4e 4x dx = 4 4 e4x + K, pues 4e 4x dx = e f(x) f (x)dx = e f(x) + K. También se puede hacer el cambio de variable t = 4x, con lo que dt = 4dx, y 4e 4x dx = e t dt = e t + K = e 4x + K, luego 4e 4x dx = 4 4 e4x + K. f) 6 x + dx = 6 x + dx = (x + ) /6 dx = 6 7 (x + )7/6 + K = 3 7 (x + )7/6 + K. Alternativamente, mediante el cambio de variable t = x +, se tiene que dt = dx, y la integral se reescribe en términos de t como t/6 dt, y t/6 dt = t /6 dt = 6 7 t7/6 + K = 3 7 (x + )7/6 + K. g) dx = dx = x 3 x 3 (x 3)/ + K = 4 (x 3)/ + K, ya que dx es una integral inmediata del x 3 tipo f (x)(f(x)) n dx con f(x) = x 3 y n =. Alternativamente, se puede hacer uso del cambio de variable t = x 3. h) x (x 3 + 4) 4 dx = 6 30 (x3 + 4) 5 + K, 6x (x 3 + 4) 4 dx = 6 5 (x3 + 4) 5 + K =
22 ya que 6x (x 3 + 4) 4 dx = f (x)(f(x)) n dx con f(x) = x y n = 4. Una forma alternativa de resolver la integral es mediante cambio de variable. Haciendo el cambio de variable t = x 3 + 4, se tiene que dt = 6x dx, y la integral se reescribe en términos de t como 6 t4 dt = 6 t 4 dt = 6 5 t5 + K = 30 (x3 + 4) 5 + K. 6 t4 dt, y i) dx (5x ) = (5x ) 3 dx = 5(5x ) 3 dx = (5x ) + K = 0 (5x ) + K. El mismo resultado se obtendría a través del cambio de variable t = 5x. j) x + 4 (x + 8x) dx = x + 8 /4 (x + 8x) dx = x + 8 dx = /4 (x + 8x) /4 (x + 8)(x + 8x) /4 dx = 4 3 (x + 8x) 3/4 + K = 3 (x + 8x) 3/4 + K. Mediante el cambio de variable t = x + 8x, dt = x + 8, y x + 4 (x + 8x) /4 dx = t /4 dt = 4 3 t3/4 + K = 3 (x + 8x) 3/4 + K. k) ( x + )( x x + )dx = ( x + x x x + )dx = ( x + x / x 3/ + )dx = x x3/ 4 5 x5/ + x + K. l) (ln x) 4 3x dx = (ln x) 4 dx = 3 x 3 5 (ln x)5 + K = 5 (ln x)5 + K, ya que (ln x) 4 dx = f (x)(f(x)) n dx con f(x) = ln x y n = 4. x Alternativamente se puede hacer el cambio t = ln x, con lo que dt = x dx, y (ln x) 4 3x dx = 3 t 4 dt = 3 5 t5 + K = 5 t5 + K = 5 (ln x)5 + K.
23 m) e x xdx = e x xdx = ex + K, pues e x xdx es inmediata, de la forma e f(x) f (x)dx, que es igual a e f(x) + K. También se puede hacer el cambio de variable t = x, con lo que dt = xdx, y e x xdx = e t dt = et + K = ex + K. n) 3x x + dx = 3 una integral inmediata de la forma f (x) K, con f(x) = x +. x x + dx = 3 ln(x + ) + K, ya que x dx es x + dx, que es igual a ln(f(x))+ f(x) También puede utilizarse el cambio de variable t = x +, con lo que dt = xdx, y 3x x + dx = 3 t dt = 3 ln(t) + K = 3 ln(x + ) + K. ñ) e 5/x x dx = 5e 5/x dx = 0 x 0 e5/x + K, pues 5e 5/x dx es una x integral inmediata de la forma f (x)e f(x) dx, que es igual a e f(x) + K, con f(x) = 5/x. Otra forma de resolverla es hacer uso del cambio de variable t = 5/x. o) x 3 x + x 4 4x + 4x dx = 4x 3 8x x 4 4x + 4x dx = 4 ln(x4 4x + 4x ) + K, de forma similar a la integral h). El cambio de variable t = x 4 4x +4x, conduce al mismo resultado. p) x [3 + ln x] 3 dx = [3 + ln x] + K, ya que es una integral inmediata del tipo f (x)(f(x)) n dx con f(x) = 3 + ln x y n = 3. También se puede hacer el cambio de variable t = 3 + ln x. q) e x ex + dx = (ex + ) / + K, pues es una integral inmediata del tipo f (x)(f(x)) n dx con f(x) = e x + y n =. De forma alternativa, resulta adecuado hacer el cambio t = e x +. 3
24 r) x( x + ) dx = x( x + ) dx = ln( x + ) + K, ya que x( x + ) dx es una integral inmediata de la forma f (x) f(x) dx, que es igual a ln(f(x)) + K, con f(x) = x +. También se puede hacer el cambio de variable t = x +. s) dx = ln(3 + ln x) + K, porque es una integral inmediata x(3 + ln x) de la forma f (x) dx, con f(x) = 3 + ln x. f(x) El mismo resultado se obtiene mediante el cambio de variable t = 3 + ln x. Ejercicio Calcular las siguientes integrales definidas: a) b) c) (x 3 x x)dx. x x + dx. ln 4 x x dx. d) x + e x +x dx. a) b) c) d) (x 3 x x)dx = x4 3 x3 x 4 x x + dx = ln (x + ) 0 = ln 3 ln. ln 4 x x dx = 5 ln5 x 3 = 5 ln5 3. x + e dx = x x +x e x = e. 4 = 86 3.
25 Ejercicio 3 Calcular el área comprendida entre la recta y = x + 4, el eje OX y el eje OY. En primer lugar se dibuja la recta y la correspondiente representación gráfica del área, que se da en la figura 3. Los puntos de corte de la recta con Figura 3: Representación gráfica del área correspondiente al ejercicio 3 los ejes son: (, 0) y (0, 4), con lo que el área que se pide es: 0 (x + 4)dx = x + 4x 0 = 4 u.a. Ejercicio 4 Calcular el área que encierra la recta y = 4, el eje OX y las rectas x = y x = 3. La representación gráfica del área buscada aparece en la figura 4, y vale: 3 4dx = 4x 3 = 0 u.a. Ejercicio 5 Hallar el área limitada por las curvas y = x 3 e y = 5 x. 5
26 Figura 4: Representación gráfica del área correspondiente al ejercicio 4 Para calcular esta área hay que dibujar ambas parábolas y calcular sus puntos de intersección. Estos puntos se obtienen a continuación: } y = x 3 y = 5 x 8 = x x =, x =. La gráfica de estas parábolas aparece en la figura 5, con lo que el área es: ] [ ] (5 x )dx (x 3)dx = [5x x3 x x = 64 3 u.a. Figura 5: Representación gráfica del área correspondiente al ejercicio 5 Ejercicio 6 Hallar el área de la región del plano limitada por las gráficas f(x) = x 3 x + y g(x) = x +. 6
27 En primer lugar hay que dibujar ambas funciones, lo que aparece en la figura 6. Una vez representadas se calculan los puntos donde se cortan. } y = x + y = x 3 x(x x ) = 0 x = 5, x = + 5 x + Se aplica la aditividad respecto del intervalo: A = : A = (x 3 x + )dx (x + )dx (x + )dx = 0, ,696 7 = 0,075 8 (x 3 x + )dx de modo que el área buscada es A = A + A. 0 (x 3 x + )dx = Figura 6: Representación gráfica del área correspondiente al ejercicio 6 Ejercicio 7 Calcular el área limitada por la curva y = x 3 x + el eje OX y las rectas x = 0 y x = 3. La gráfica de la parábola se encuentra en la figura 7, y los puntos de corte de la curva dada con el eje OX son: x 3 x + = 0 x =, x =. 7
28 Entonces el área pedida es: A = 0 ( x 3 x + )dx ( x 3 3 x + )dx + ( x 3 x + )dx = [ x 3 = x + x ] 0 [ x x + x ] [ x x + x ] 3 = u.a. Figura 7: Representación gráfica del área correspondiente al ejercicio 7 Ejercicio 8 Calcular el área del recinto limitado por la parábola de ecuación y = 4 x y la recta y = x +. Hacer una representación gráfica aproximada de dicha área. Los puntos de corte de la parábola y la recta son: } 3x + x 6 = y x =, x =. x + = y Y la representación gráfica del área se encuentra en la figura 8. Entonces el área pedida es: ] [ ] A = (4 x )dx (x + )dx = [4x x3 x x = 9 u.a. Ejercicio 9 Calcular el área comprendida entre la curva y = 3x +x 6, el eje OX y las rectas x = y x = 4. Hacer una representación gráfica aproximada de dicha área. 8
29 Figura 8: Representación gráfica del área correspondiente al ejercicio 8 Los puntos de corte de la curva dada con el eje OX son: 3x + x 6 = 0 x =, x = 8 3. Y la representación gráfica se encuentra en la figura 9. Así, el área pedida es: A = (3x + x 6)dx + 4 (3x + x 6)dx = = [ x 3 + x 6x ] + [ x + x 6x ] 4 = 84 u.a. Figura 9: Representación gráfica del área correspondiente al ejercicio 9 Ejercicio 0 Calcular el área del recinto limitado por la parábola de ecuación y = x + 8x y el eje OX. 9
30 Los puntos de corte de la curva dada con el eje OX: x + 8x = 0 x = 0, x = 8. Y la representación gráfica de la parábola se da en la figura 0, con lo que el área pedida es: 8 ] 8 A = ( x + 8x)dx = [ x x = u.a. Figura 0: Representación gráfica del área correspondiente al ejercicio 0 4. Ejercicios propuestos Ejercicio Hallar las funciones derivadas de las siguientes funciones: a) f(x) = x 5. b) f(x) = 3x 4. c) f(x) = x 4 + x 3 x 3 x. d) f(x) = 3x. e) f(x) = x ln x. f) f(x) = (x 3 3x 4 )e x. 30
31 g) f(x) = x3 + x. ln x h) f(x) = e x3 7x+. i) f(x) = (5x x) e x4 3x. j) f(x) = k) f(x) = ln a) f (x) = 5x 4. b) f (x) = x 3. x 3 3x +. ( ) x. 5x + c) f (x) = 8x 3 + 3x 4x + 3 x. d) f (x) = 3 3x. e) f (x) = x + x ln x. f) f (x) = e x (3x x 3 3x 4 ). g) f (x) = 3x + 4x ln x x + x (ln x). h) f (x) = e x3 7x+ (3x 7). i) f (x) = e x4 3x (0x ) + e x4 3x (5x x) (4x 3 3). x 3 j) f (x) = 3 ( ) 3. 3x + 3x + 3x + k) f (x) = x 5 5x +. Ejercicio Para las funciones siguientes, estudiar su crecimiento y sus extremos relativos: a) f(x) = x 3x +. x 3
32 b) f(x) = 3 x3 + 5 x 6x + 7. c) f(x) = x. x a) f(x) es creciente en (3/4, + ) y decreciente en (, 3/4).En x = 3/4, la función tiene un mínimo relativo. b) f(x) es creciente si x (, 6) (, + ) y decreciente si x ( 6, ). c) f es decreciente para x (, ) (, + ) y creciente para x (, 0) (0, ).Tiene un mínimo relativo en x = y un máximo relativo en x =. Ejercicio 3 Realizar las siguientes integrales indefinidas: a) (x 5 + 4x 3 x + 5)dx. b) ( 5 x + x)dx. c) ( 3x + 5x)dx. d) 7x + 4dx. e) e 6x dx. f) 4 4x + dx. g) 5x dx. h) x 3 (3x 4 + ) 5 dx. i) 6 4x dx. j) dx (3x + 3) 4. k) x + 3 dx. (x + 6x) /5 l) ( x )( x x)dx. 3
33 m) (ln x) 5 4x dx. n) e x +5 xdx. ñ) 4x x 7 dx. o) e /x 3x dx. p) x 3 4x + x 4 4x + 4x dx. q) x [ + ln x] 4 dx. a) 6 x6 + x 4 x + 5x + K. b) 5x x 3 + K. 6 3 c) ln x x + K. d) (7x + 4) 3 + K. e) 6 e6x + K. f) 5 (4x + ) K. g) 5 5x + K. h) 7 (3x4 + ) 6 + K i) 6 8 (4x )7/6 + K. j) 9 (3x + 3) 3 + K. k) 5 8 (x + 6x) 4/5 + K. l) 5 x 3 (6x 5 x + 0) + K. m) 4 ln6 x + K. 33
34 n) +5 ex + K. ñ) ln (x 7) + K. o) 6 e/x + K. p) ln (x4 4x + 4x ) + K. q) 6 (ln x + ) 3 + K. Ejercicio 4 Calcular las siguientes integrales definidas: a) b) c) d) e) (x 5 3x 3)dx. 4 3x dx. ( 3 x + x)dx. 4x x dx. ln 5 x x dx. a) b) 4 3 ln. c) d) ln 3 4 ln. e) 6 ln6. Ejercicio 5 Calcular el área comprendida entre la curva y = x x, el eje OX y las rectas x = y x =. 34
35 Ejercicio 6 Calcular el área comprendida entre las curvas y = x x 4, el eje OX e y = x 4x
Límites y continuidad de funciones reales de variable real
 Límites y continuidad de funciones reales de variable real Álvarez S., Caballero M.V. y Sánchez M. a M. salvarez@um.es, m.victori@um.es, marvega@um.es Índice 1. Definiciones 3 2. Herramientas 10 2.1. Funciones
Límites y continuidad de funciones reales de variable real Álvarez S., Caballero M.V. y Sánchez M. a M. salvarez@um.es, m.victori@um.es, marvega@um.es Índice 1. Definiciones 3 2. Herramientas 10 2.1. Funciones
MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES
 MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES CAPÍTULO 5 Curso preparatorio de la prueba de acceso a la universidad para mayores de 25 años curso 2010/11 Nuria Torrado Robles Departamento de Estadística Universidad
MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES CAPÍTULO 5 Curso preparatorio de la prueba de acceso a la universidad para mayores de 25 años curso 2010/11 Nuria Torrado Robles Departamento de Estadística Universidad
INTEGRAL DEFINIDA. APLICACIONES
 COLEGIO SAN ALBERTO MAGNO MATEMÁTICAS II INTEGRAL DEFINIDA. APLICACIONES. 008 MODELO OPCIÓN A. Ejercicio. [ 5 puntos] Dadas las funciones f : [0,+ ) R y g : [0, + ) R definidas por y calcula el área del
COLEGIO SAN ALBERTO MAGNO MATEMÁTICAS II INTEGRAL DEFINIDA. APLICACIONES. 008 MODELO OPCIÓN A. Ejercicio. [ 5 puntos] Dadas las funciones f : [0,+ ) R y g : [0, + ) R definidas por y calcula el área del
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 004 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 004 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
Estudio de funciones mediante límites y derivadas
 Estudio de funciones mediante límites y derivadas CVS0. El precio del billete de una línea de autobús se obtiene sumando dos cantidades, una fija y otra proporcional a los kilómetros recorridos. Por un
Estudio de funciones mediante límites y derivadas CVS0. El precio del billete de una línea de autobús se obtiene sumando dos cantidades, una fija y otra proporcional a los kilómetros recorridos. Por un
TEMA 7 INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES 7.1 CRECIMIENTO DE UNA FUNCIÓN EN UN INTERVALO
 TEMA 7 DERIVADAS Y APLICACIONES MATEMÁTICAS CCSSI º Bac TEMA 7 INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES 7. CRECIMIENTO DE UNA FUNCIÓN EN UN INTERVALO TASA DE VARIACIÓN MEDIA Definición : Se llama
TEMA 7 DERIVADAS Y APLICACIONES MATEMÁTICAS CCSSI º Bac TEMA 7 INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES 7. CRECIMIENTO DE UNA FUNCIÓN EN UN INTERVALO TASA DE VARIACIÓN MEDIA Definición : Se llama
1.- Entre todos los triángulos rectángulos de 5 metros de hipotenusa, determina los catetos del de área máxima. Solución:
 RELACIÓN DE PROBLEMAS DE SELECTIVIDAD DE ANÁLISIS. I Departamento de Matemáticas 1.- Entre todos los triángulos rectángulos de 5 metros de hipotenusa, determina los catetos del de área máxima. Función
RELACIÓN DE PROBLEMAS DE SELECTIVIDAD DE ANÁLISIS. I Departamento de Matemáticas 1.- Entre todos los triángulos rectángulos de 5 metros de hipotenusa, determina los catetos del de área máxima. Función
Colegio Portocarrero. Curso Departamento de matemáticas. Análisis. (Límites/Asíntotas/Continuidad/Derivadas/Aplicaciones de las derivadas)
 Análisis (Límites/Asíntotas/Continuidad/Derivadas/Aplicaciones de las derivadas) Problema 1: Sea la función Determina: a) El dominio de definición. b) Las asíntotas si existen. c) El o los intervalos de
Análisis (Límites/Asíntotas/Continuidad/Derivadas/Aplicaciones de las derivadas) Problema 1: Sea la función Determina: a) El dominio de definición. b) Las asíntotas si existen. c) El o los intervalos de
ACTIVIDADES SELECTIVIDAD APLICACIONES DERIVADAS
 ACTIVIDADES SELECTIVIDAD APLICACIONES DERIVADAS Ejercicio 1 De la función se sabe que tiene un máximo en, y que su gráfica corta al eje OX en el punto de abscisa y tiene un punto de inflexión en el punto
ACTIVIDADES SELECTIVIDAD APLICACIONES DERIVADAS Ejercicio 1 De la función se sabe que tiene un máximo en, y que su gráfica corta al eje OX en el punto de abscisa y tiene un punto de inflexión en el punto
PROBLEMAS DE INTEGRALES INDEFINIDAS
 PROBLEMAS DE INTEGRALES INDEFINIDAS Integración por partes. Mediante la integración por partes, hallar una primitiva de la función y = Ln (1 + x) Calcular una primitiva de una función, es hallar su
PROBLEMAS DE INTEGRALES INDEFINIDAS Integración por partes. Mediante la integración por partes, hallar una primitiva de la función y = Ln (1 + x) Calcular una primitiva de una función, es hallar su
CBC. Matemática (51) universoexacto.com 1
 CBC Matemática (51) universoexacto.com 1 PROGRAMA ANALÍTICO 1 :: UNIDAD 1 Números Reales y Coordenadas Cartesianas Representación de los números reales en una recta. Intervalos de Distancia en la recta
CBC Matemática (51) universoexacto.com 1 PROGRAMA ANALÍTICO 1 :: UNIDAD 1 Números Reales y Coordenadas Cartesianas Representación de los números reales en una recta. Intervalos de Distancia en la recta
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2001 MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PRIMITIVAS E INTEGRAL DEFINIDA Ejercicios de selectividad
 PRIMITIVAS E INTEGRAL DEFINIDA Ejercicios de selectividad Sea f : R R la función definida por f() = e /. (a) En qué punto de la gráfica de f la recta tangente a ésta pasa por el origen de coordenadas?
PRIMITIVAS E INTEGRAL DEFINIDA Ejercicios de selectividad Sea f : R R la función definida por f() = e /. (a) En qué punto de la gráfica de f la recta tangente a ésta pasa por el origen de coordenadas?
4. ANÁLISIS DE FUNCIONES DE UNA VARIABLE
 Análisis de funciones de una variable 49 4. ANÁLISIS DE FUNCIONES DE UNA VARIABLE En esta sección realizaremos algunos ejercicios sobre el estudio de funciones de una variable: En la parte final hay ejercicios
Análisis de funciones de una variable 49 4. ANÁLISIS DE FUNCIONES DE UNA VARIABLE En esta sección realizaremos algunos ejercicios sobre el estudio de funciones de una variable: En la parte final hay ejercicios
UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD
 Opción A xcos(x)+b sen(x) Ejercicio 1.- [2 5 puntos] Sabiendo que lím x 0 x 3 es finito, calcula b y el valor del límite. Ejercicio 2.- Sean f : R R y g : R R las funciones definidas mediante f(x) = x(x
Opción A xcos(x)+b sen(x) Ejercicio 1.- [2 5 puntos] Sabiendo que lím x 0 x 3 es finito, calcula b y el valor del límite. Ejercicio 2.- Sean f : R R y g : R R las funciones definidas mediante f(x) = x(x
12.1 CRECIMIENTO DE UNA FUNCIÓN EN UN INTERVALO
 INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES. CRECIMIENTO DE UNA FUNCIÓN EN UN INTERVALO TASA DE VARIACIÓN MEDIA Deinición Se llama tasa de variación media (T.V.M.) de una unción, y = () en un intervalo
INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES. CRECIMIENTO DE UNA FUNCIÓN EN UN INTERVALO TASA DE VARIACIÓN MEDIA Deinición Se llama tasa de variación media (T.V.M.) de una unción, y = () en un intervalo
APLICACIONES DE LA DERIVADA
 APLICACIONES DE LA DERIVADA Ejercicio -Sea f: R R la función definida por f ( ) = + a + b + a) [ 5 puntos] Determina a, b R sabiendo que la gráfica de f pasa por el punto (, ) y tiene un punto de infleión
APLICACIONES DE LA DERIVADA Ejercicio -Sea f: R R la función definida por f ( ) = + a + b + a) [ 5 puntos] Determina a, b R sabiendo que la gráfica de f pasa por el punto (, ) y tiene un punto de infleión
PROBLEMAS DE OPTIMIZACIÓN
 1 PROBLEMAS DE OPTIMIZACIÓN Planteamiento y resolución de los problemas de optimización Se quiere construir una caja, sin tapa, partiendo de una lámina rectangular de cm de larga por de ancha. Para ello
1 PROBLEMAS DE OPTIMIZACIÓN Planteamiento y resolución de los problemas de optimización Se quiere construir una caja, sin tapa, partiendo de una lámina rectangular de cm de larga por de ancha. Para ello
Problemas de Selectividad de Matemáticas II Comunidad de Madrid (Resueltos) Isaac Musat Hervás
 Problemas de Selectividad de Matemáticas II Comunidad de Madrid Resueltos Isaac Musat Hervás 22 de mayo de 213 Capítulo 11 Año 21 11.1. Modelo 21 - Opción A Problema 11.1.1 3 puntos Dada la función: fx
Problemas de Selectividad de Matemáticas II Comunidad de Madrid Resueltos Isaac Musat Hervás 22 de mayo de 213 Capítulo 11 Año 21 11.1. Modelo 21 - Opción A Problema 11.1.1 3 puntos Dada la función: fx
PAU Madrid. Matemáticas II. Año Examen modelo. Opción A. Ejercicio 1. Valor: 2 puntos.
 PAU Madrid. Matemáticas II. Año 22. Examen modelo. Opción A. Ejercicio 1. Valor: 2 puntos. Se considera una varilla AB de longitud 1. El extremo A de esta varilla recorre completamente la circunferencia
PAU Madrid. Matemáticas II. Año 22. Examen modelo. Opción A. Ejercicio 1. Valor: 2 puntos. Se considera una varilla AB de longitud 1. El extremo A de esta varilla recorre completamente la circunferencia
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2012 MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 0 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 0 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
IES Fco Ayala de Granada Junio de 2012 (Común Modelo 4) Soluciones Germán-Jesús Rubio Luna
 IES Fco Ayala de Granada Junio de 01 (Común Modelo 4) Soluciones Germán-Jesús Rubio Luna Opción A Ejercicio 1 opción A, modelo Junio 01 común Sea f : R R la función definida como f(x) = e x.(x ). [1 punto]
IES Fco Ayala de Granada Junio de 01 (Común Modelo 4) Soluciones Germán-Jesús Rubio Luna Opción A Ejercicio 1 opción A, modelo Junio 01 común Sea f : R R la función definida como f(x) = e x.(x ). [1 punto]
MATEMÁTICAS para estudiantes de primer curso de facultades y escuelas técnicas
 Universidad de Cádiz Departamento de Matemáticas MATEMÁTICAS para estudiantes de primer curso de facultades y escuelas técnicas Tema Representación gráfica de funciones reales de una variable real Elaborado
Universidad de Cádiz Departamento de Matemáticas MATEMÁTICAS para estudiantes de primer curso de facultades y escuelas técnicas Tema Representación gráfica de funciones reales de una variable real Elaborado
2 ln x dx. Solución: Resolvemos la integral por partes. Si hacemos u = ln x y dv = dx, entonces u =ln x du = 1 x dx dv = dx v = x y por tanto
 Tema 6 Integración Definida Ejercicios resueltos Ejercicio Calcular la integral definida ln x dx Solución: Resolvemos la integral por partes. Si hacemos u = ln x y dv = dx, entonces u =ln x du = x dx dv
Tema 6 Integración Definida Ejercicios resueltos Ejercicio Calcular la integral definida ln x dx Solución: Resolvemos la integral por partes. Si hacemos u = ln x y dv = dx, entonces u =ln x du = x dx dv
IES Fco Ayala de Granada Junio de 2011 (Específico Modelo 5) Solución Germán-Jesús Rubio Luna. Opción A
 IES Fco Ayala de Granada Junio de 2011 (Específico Modelo 5) Germán-Jesús Rubio Luna Opción A Ejercicio 1 opción A, modelo Junio 2011 específico1 [2'5 puntos] Un alambre de 100 m de longitud se divide
IES Fco Ayala de Granada Junio de 2011 (Específico Modelo 5) Germán-Jesús Rubio Luna Opción A Ejercicio 1 opción A, modelo Junio 2011 específico1 [2'5 puntos] Un alambre de 100 m de longitud se divide
a) Calcula el valor de k. b) Halla la ecuación de la recta tangente a la gráfica de la función f en el punto de abscisa x = 1.
 Selectividad CCNN 0. [ANDA] [JUN-A] Sea la función f: definida por f(x) = e x (x - ). a) Calcula la asíntotas de f. b) Halla los extremos relativos (abscisas donde se obtienen y valores que se alcanzan)
Selectividad CCNN 0. [ANDA] [JUN-A] Sea la función f: definida por f(x) = e x (x - ). a) Calcula la asíntotas de f. b) Halla los extremos relativos (abscisas donde se obtienen y valores que se alcanzan)
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2015 MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 05 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 05 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
Funciones reales. Números complejos
 Funciones reales. Números complejos Funciones reales 1. Encuentra todos los números reales x que verifican: a) (x 1)(x 3) > 1 b) x + 1 > 1 1 x c) x 1 + x + 1 < 1 d) 5 < x 2 14x + 5 < 26 2. Si la gráfica
Funciones reales. Números complejos Funciones reales 1. Encuentra todos los números reales x que verifican: a) (x 1)(x 3) > 1 b) x + 1 > 1 1 x c) x 1 + x + 1 < 1 d) 5 < x 2 14x + 5 < 26 2. Si la gráfica
REPRESENTACIÓN GRÁFICA DE UNA FUNCIÓN.. Se pide: x
 1 REPRESENTACIÓN GRÁFICA DE UNA FUNCIÓN IBJ05 1. Se considera la función f ( ). Se pide: a) Encontrar los intervalos donde esta función es creciente y donde es decreciente. ( puntos) b) Calcular las asíntotas.
1 REPRESENTACIÓN GRÁFICA DE UNA FUNCIÓN IBJ05 1. Se considera la función f ( ). Se pide: a) Encontrar los intervalos donde esta función es creciente y donde es decreciente. ( puntos) b) Calcular las asíntotas.
I. E. S. ATENEA. SAN SEBASTIÁN DE LOS REYES EXAMEN GLOBAL. PRIMERA EVALUACIÓN. ANÁLISIS
 Eamen Global Análisis Matemáticas II Curso 010-011 I E S ATENEA SAN SEBASTIÁN DE LOS REYES EXAMEN GLOBAL PRIMERA EVALUACIÓN ANÁLISIS Curso 010-011 1-I-011 MATERIA: MATEMÁTICAS II INSTRUCCIONES GENERALES
Eamen Global Análisis Matemáticas II Curso 010-011 I E S ATENEA SAN SEBASTIÁN DE LOS REYES EXAMEN GLOBAL PRIMERA EVALUACIÓN ANÁLISIS Curso 010-011 1-I-011 MATERIA: MATEMÁTICAS II INSTRUCCIONES GENERALES
dada por c(x) = donde x indica el tamaño de los pedidos para renovar existencias
 FUNCIONES +, si
FUNCIONES +, si
Aplicaciones de la integral definida al cálculo de áreas
 Aplicaciones de la integral definida al cálculo de áreas 1º) Interpreta geométricamente el área que define la integral y obtenla. Geométricamente, la integral representa el área de la región del plano
Aplicaciones de la integral definida al cálculo de áreas 1º) Interpreta geométricamente el área que define la integral y obtenla. Geométricamente, la integral representa el área de la región del plano
UNIDAD 4: FUNCIONES POLINOMIALES Y RACIONALES
 UNIDAD 4: FUNCIONES POLINOMIALES Y RACIONALES En la Sección anterior se abordó contenidos relacionados con las funciones y gráficas, continuamos aprendiendo más sobre funciones; en la presente unidad abordaremos
UNIDAD 4: FUNCIONES POLINOMIALES Y RACIONALES En la Sección anterior se abordó contenidos relacionados con las funciones y gráficas, continuamos aprendiendo más sobre funciones; en la presente unidad abordaremos
x = 0, la recta tangente a la gráfica de f (x)
 CÁLCULO DIFERENCIAL JUNIO 004 1. Sea la función e y = estúdiese su monotonía, etremos relativos y asíntotas. (Solución: Es derivable en todos los puntos ecepto en =0. Creciente si < 0. No tiene asíntotas
CÁLCULO DIFERENCIAL JUNIO 004 1. Sea la función e y = estúdiese su monotonía, etremos relativos y asíntotas. (Solución: Es derivable en todos los puntos ecepto en =0. Creciente si < 0. No tiene asíntotas
Estudio de funciones mediante límites y derivadas
 Estudio de funciones mediante límites y derivadas Observación: La mayoría de estos ejercicios se han propuesto en las pruebas de Selectividad, en los distintos distritos universitarios españoles El precio
Estudio de funciones mediante límites y derivadas Observación: La mayoría de estos ejercicios se han propuesto en las pruebas de Selectividad, en los distintos distritos universitarios españoles El precio
REPRESENTACIÓN DE FUNCIONES
 8 REPRESENTACIÓN DE FUNCIONES Página 86 Descripción de una gráfica. Copia en tu cuaderno los datos encuadrados en rojo. A partir de ellos y sin mirar la gráfica que aparece al principio, representa esta
8 REPRESENTACIÓN DE FUNCIONES Página 86 Descripción de una gráfica. Copia en tu cuaderno los datos encuadrados en rojo. A partir de ellos y sin mirar la gráfica que aparece al principio, representa esta
DERIVACIÓN DE LAS FUNCIONES ELEMENTALES
 DERIVACIÓN DE LAS FUNCIONES ELEMENTALES 2 El procedimiento mediante el cuál se obtiene la derivada de una función se conoce como derivación. Llamaremos funciones elementales a las funciones polinómicas,
DERIVACIÓN DE LAS FUNCIONES ELEMENTALES 2 El procedimiento mediante el cuál se obtiene la derivada de una función se conoce como derivación. Llamaremos funciones elementales a las funciones polinómicas,
www.academiacae.com!!info@academiacae.com!!91.501.36.88!!28007!madrid!
 CONTINUIDAD Y DERIVABILIDAD. TEOREMAS Y APLICACIONES DE LAS DERIVADAS 1.- junio 1994 Se sabe que y = f (x) e y = g (x) son dos curvas crecientes en x = a. Analícese si la curva y = f(x) g(x) ha de ser,
CONTINUIDAD Y DERIVABILIDAD. TEOREMAS Y APLICACIONES DE LAS DERIVADAS 1.- junio 1994 Se sabe que y = f (x) e y = g (x) son dos curvas crecientes en x = a. Analícese si la curva y = f(x) g(x) ha de ser,
TEMA 12 INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES 12.1 CRECIMIENTO DE UNA FUNCIÓN EN UN INTERVALO
 TEMA DERIVADAS Y APLICACIONES MATEMÁTICAS I º Bac TEMA INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES. CRECIMIENTO DE UNA FUNCIÓN EN UN INTERVALO TASA DE VARIACIÓN MEDIA Deinición Se llama tasa de variación
TEMA DERIVADAS Y APLICACIONES MATEMÁTICAS I º Bac TEMA INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES. CRECIMIENTO DE UNA FUNCIÓN EN UN INTERVALO TASA DE VARIACIÓN MEDIA Deinición Se llama tasa de variación
= 1. x = 3: Lím = Asíntota vertical en x = 3: = 0 ; No se anula nunca. Punto de corte con OY es (0, 3) 3 x
 Modelo 4. Problema A.- (Calificación máima: puntos) 4 si Se considera la función real de variable real f ( ) si > a) Determínense las asíntotas de la función y los puntos de corte con los ejes. a. Asíntotas
Modelo 4. Problema A.- (Calificación máima: puntos) 4 si Se considera la función real de variable real f ( ) si > a) Determínense las asíntotas de la función y los puntos de corte con los ejes. a. Asíntotas
IES Francisco Ayala Modelo 1 (Septiembre) de 2007 Solución Germán Jesús Rubio Luna. Opción A
 IES Francisco Ayala Modelo (Septiembre) de 7 Germán Jesús Rubio Luna Opción A Ejercicio n de la opción A de septiembre, modelo de 7 3x+ Sea f: (,+ ) R la función definida por f(x)= x. [ 5 puntos] Determina
IES Francisco Ayala Modelo (Septiembre) de 7 Germán Jesús Rubio Luna Opción A Ejercicio n de la opción A de septiembre, modelo de 7 3x+ Sea f: (,+ ) R la función definida por f(x)= x. [ 5 puntos] Determina
DERIVADAS. Para hallar la pendiente de una curva en algún punto hacemos uso de la recta tangente de una curva en un punto.
 DERIVADAS Tema: La derivada como pendiente de una curva Para hallar la pendiente de una curva en algún punto hacemos uso de la recta tangente de una curva en un punto. La pendiente de la curva en el punto
DERIVADAS Tema: La derivada como pendiente de una curva Para hallar la pendiente de una curva en algún punto hacemos uso de la recta tangente de una curva en un punto. La pendiente de la curva en el punto
IES Fco Ayala de Granada Septiembre de 2011 (Septiembre Modelo 2) Solución Germán-Jesús Rubio Luna
 IES Fco Ayala de Granada Septiembre de 0 (Septiembre Modelo ) Germán-Jesús Rubio Luna UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD CURSO 00-0. MATEMÁTICAS II Opción A Ejercicio opción A,
IES Fco Ayala de Granada Septiembre de 0 (Septiembre Modelo ) Germán-Jesús Rubio Luna UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD CURSO 00-0. MATEMÁTICAS II Opción A Ejercicio opción A,
1. INTEGRALES DEFINIDAS E IMPROPIAS
 . INTEGRALES DEFINIDAS E IMPROPIAS. Hallar el área de la región limitada por la parábola y = y el eje OX. Los cortes de la gráfica de y = con el eje OX son los valores de tales que =, esto es, = y =. El
. INTEGRALES DEFINIDAS E IMPROPIAS. Hallar el área de la región limitada por la parábola y = y el eje OX. Los cortes de la gráfica de y = con el eje OX son los valores de tales que =, esto es, = y =. El
UNIVERSIDAD NACIONAL DE GENERAL SARMIENTO Matemática I Segundo Parcial (21/11/09) xe2x JUSTIFIQUE TODAS SUS RESPUESTAS
 Segundo Parcial (21/11/09) 1. Sea f(x) = 1 +2 xe2x a) Hallar dominio, intervalos de crecimiento y decrecimiento y extremos locales de f. b) Hallar (si las hay) las asíntotas horizontales y verticales de
Segundo Parcial (21/11/09) 1. Sea f(x) = 1 +2 xe2x a) Hallar dominio, intervalos de crecimiento y decrecimiento y extremos locales de f. b) Hallar (si las hay) las asíntotas horizontales y verticales de
Tema 1. Cálculo diferencial
 Tema 1. Cálculo diferencial 1 / 57 Una función es una herramienta mediante la que expresamos la relación entre una causa (variable independiente) y un efecto (variable dependiente). Las funciones nos permiten
Tema 1. Cálculo diferencial 1 / 57 Una función es una herramienta mediante la que expresamos la relación entre una causa (variable independiente) y un efecto (variable dependiente). Las funciones nos permiten
UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD
 Opción A Ejercicio 1.- [2 5 puntos] Una ventana normanda consiste en un rectángulo coronado con un semicírculo. De entre todas las ventanas normandas de perímetro 10 m, halla las dimensiones del marco
Opción A Ejercicio 1.- [2 5 puntos] Una ventana normanda consiste en un rectángulo coronado con un semicírculo. De entre todas las ventanas normandas de perímetro 10 m, halla las dimensiones del marco
PRUEBAS DE ACCESO A LA UNIVERSIDAD EJERCICIOS RESUELTOS DEL BLOQUE DE ANÁLISIS
 PRUEBAS DE ACCESO A LA UNIVERSIDAD EJERCICIOS RESUELTOS DEL BLOQUE DE ANÁLISIS MODELO 2000: OPCIÓN A: a. Calcúlense p y q de modo que la curva y = x $ + px + q contenga al punto ( 2, 1) y presente un mínimo
PRUEBAS DE ACCESO A LA UNIVERSIDAD EJERCICIOS RESUELTOS DEL BLOQUE DE ANÁLISIS MODELO 2000: OPCIÓN A: a. Calcúlense p y q de modo que la curva y = x $ + px + q contenga al punto ( 2, 1) y presente un mínimo
«La derivada de una función en un punto representa geométricamente la pendiente de la recta tangente a la función en dicho punto»
 TEMA 10 DERIVADA DE UNA FUNCIÓN EN UN PUNTO f (a): Consideremos una función f(x) y un punto P de su gráfica (ver figura), de abscisa x=a. Supongamos que damos a la variable independiente x un pequeño incremento
TEMA 10 DERIVADA DE UNA FUNCIÓN EN UN PUNTO f (a): Consideremos una función f(x) y un punto P de su gráfica (ver figura), de abscisa x=a. Supongamos que damos a la variable independiente x un pequeño incremento
CONTINUIDAD DE FUNCIONES. SECCIONES A. Definición de función continua. B. Propiedades de las funciones continuas. C. Ejercicios propuestos.
 CAPÍTULO IV. CONTINUIDAD DE FUNCIONES SECCIONES A. Definición de función continua. B. Propiedades de las funciones continuas. C. Ejercicios propuestos. 121 A. DEFINICIÓN DE FUNCIÓN CONTINUA. Una función
CAPÍTULO IV. CONTINUIDAD DE FUNCIONES SECCIONES A. Definición de función continua. B. Propiedades de las funciones continuas. C. Ejercicios propuestos. 121 A. DEFINICIÓN DE FUNCIÓN CONTINUA. Una función
IES Fco Ayala de Granada Septiembre de 2015 (Modelo 3) Soluciones Germán-Jesús Rubio Luna. Opción A. Ejercicio 1 opción A, modelo 3 Septiembre
 IES Fco Ayala de Granada Septiembre de 015 (Modelo 3) Soluciones Germán-Jesús Rubio Luna Opción A Ejercicio 1 opción A, modelo 3 Septiembre 015 ax + b [ 5 puntos] Halla los valores a, b y c sabiendo que
IES Fco Ayala de Granada Septiembre de 015 (Modelo 3) Soluciones Germán-Jesús Rubio Luna Opción A Ejercicio 1 opción A, modelo 3 Septiembre 015 ax + b [ 5 puntos] Halla los valores a, b y c sabiendo que
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2006 MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 006 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 006 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
La variable independiente x es aquella cuyo valor se fija previamente. La variable dependiente y es aquella cuyo valor se deduce a partir de x.
 Bloque 8. FUNCIONES. (En el libro Temas 10, 11 y 12, páginas 179, 197 y 211) 1. Definiciones: función, variables, ecuación, tabla y gráfica. 2. Características o propiedades de una función: 2.1. Dominio
Bloque 8. FUNCIONES. (En el libro Temas 10, 11 y 12, páginas 179, 197 y 211) 1. Definiciones: función, variables, ecuación, tabla y gráfica. 2. Características o propiedades de una función: 2.1. Dominio
b) Para encontrar los intervalos de crecimiento y decrecimiento, hay que derivar la función. Como que se trata de un cociente, aplicamos la fórmula:
 1. Dada la función f(x) = : a) Encontrar el dominio, las AH y las AV. b) Intervalos de crecimiento, decrecimiento, máximos y mínimos relativos. c) Primitiva que cumpla que F(0) = 0. a) Para encontrar el
1. Dada la función f(x) = : a) Encontrar el dominio, las AH y las AV. b) Intervalos de crecimiento, decrecimiento, máximos y mínimos relativos. c) Primitiva que cumpla que F(0) = 0. a) Para encontrar el
Apuntes de dibujo de curvas
 Apuntes de dibujo de curvas El objetivo de estas notas es dar unas nociones básicas sobre dibujo de curvas definidas por medio de ecuaciones cartesianas explícitas o paramétricas y polares: 1. Curvas en
Apuntes de dibujo de curvas El objetivo de estas notas es dar unas nociones básicas sobre dibujo de curvas definidas por medio de ecuaciones cartesianas explícitas o paramétricas y polares: 1. Curvas en
Matemáticas Febrero 2013 Modelo A
 Matemáticas Febrero 0 Modelo A. Calcular el rango de 0 0 0. 0 a) b) c). Cuál es el cociente de dividir P(x) = x x + 9 entre Q(x) = x +? a) x x + x 6. b) x + x + x + 6. c) x x + 5x 0.. Diga cuál de las
Matemáticas Febrero 0 Modelo A. Calcular el rango de 0 0 0. 0 a) b) c). Cuál es el cociente de dividir P(x) = x x + 9 entre Q(x) = x +? a) x x + x 6. b) x + x + x + 6. c) x x + 5x 0.. Diga cuál de las
TEMA 12 INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES
 Tema Derivadas. Aplicaciones Matemáticas I º Bacillerato TEMA INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES TASA DE VARIACIÓN MEDIA DE UNA FUNCIÓN EN UN INTERVALO EJERCICIO : Halla la tasa de variación
Tema Derivadas. Aplicaciones Matemáticas I º Bacillerato TEMA INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES TASA DE VARIACIÓN MEDIA DE UNA FUNCIÓN EN UN INTERVALO EJERCICIO : Halla la tasa de variación
Funciones 1. D = Dom ( f ) = x R / f(x) R. Recuerda como determinabas los dominios de algunas funciones: x x
 Funciones. DEFINICIÓN Y TERMINOLOGÍA.. Definición de función real de variable real. "Es toda correspondencia, f, entre un subconjunto D de números reales y R (o una parte de R), con la condición de que
Funciones. DEFINICIÓN Y TERMINOLOGÍA.. Definición de función real de variable real. "Es toda correspondencia, f, entre un subconjunto D de números reales y R (o una parte de R), con la condición de que
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2012 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 01 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva 1, Ejercicio, Opción A Reserva
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 01 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva 1, Ejercicio, Opción A Reserva
Matemáticas II PRUEBA DE ACCESO A LA UNIVERSIDAD 2012 BACHILLERATO FORMACIÓN PROFESIONAL CICLOS FORMATIVOS DE GRADO SUPERIOR.
 PRUEBA DE ACCESO A LA UNIVERSIDAD 2012 Matemáticas II BACHILLERATO FORMACIÓN PROFESIONAL CICLOS FORMATIVOS DE GRADO SUPERIOR Examen Criterios de Corrección y Calificación UNIBERTSITATERA SARTZEKO PROBAK
PRUEBA DE ACCESO A LA UNIVERSIDAD 2012 Matemáticas II BACHILLERATO FORMACIÓN PROFESIONAL CICLOS FORMATIVOS DE GRADO SUPERIOR Examen Criterios de Corrección y Calificación UNIBERTSITATERA SARTZEKO PROBAK
5 Demostrar cada una de las siguientes afirmaciones empleando la definición de
 Hallar el dominio de las siguientes funciones: x 3 a) x +ln(x ) b) ln x + 6 x + c) x x d) ln x x + e) cos x + ln(x 5π) + 8π x Graficar la función sen(x π ). Hallar para que valores de x es 3 Hallar las
Hallar el dominio de las siguientes funciones: x 3 a) x +ln(x ) b) ln x + 6 x + c) x x d) ln x x + e) cos x + ln(x 5π) + 8π x Graficar la función sen(x π ). Hallar para que valores de x es 3 Hallar las
IES Fco Ayala de Granada Sobrantes de 2011 (Modelo 4) Soluciones Germán-Jesús Rubio Luna
 IES Fco Ayala de Granada Sobrantes de 011 (Modelo 4) Soluciones Germán-Jesús Rubio Luna Opción A Ejercicio 1 opción A, modelo 4 del 011 [ 5 puntos] Queremos hacer junto a la carretera un cercado rectangular
IES Fco Ayala de Granada Sobrantes de 011 (Modelo 4) Soluciones Germán-Jesús Rubio Luna Opción A Ejercicio 1 opción A, modelo 4 del 011 [ 5 puntos] Queremos hacer junto a la carretera un cercado rectangular
COL LECCIÓ DE PROBLEMES RESOLTS
 DEPARTAMENT DE MATEMÀTICA ECONOMICOEMPRESARIAL DEPARTAMENT D ECONOMIA FINANCERA UNIVERSITAT DE VALÈNCIA LLICENCIATURA EN ECONOMIA LLICENCIATURA EN ADMINISTRACIÓ I DIRECCIÓ D EMPRESES DIPLOMATURA EN CIÈNCIES
DEPARTAMENT DE MATEMÀTICA ECONOMICOEMPRESARIAL DEPARTAMENT D ECONOMIA FINANCERA UNIVERSITAT DE VALÈNCIA LLICENCIATURA EN ECONOMIA LLICENCIATURA EN ADMINISTRACIÓ I DIRECCIÓ D EMPRESES DIPLOMATURA EN CIÈNCIES
REPRESENTACIÓN DE FUNCIONES
 REPRESENTACIÓN DE FUNCIONES Página 5 REFLEXIONA Y RESUELVE Descripción de una gráfica Copia en tu cuaderno los datos encuadrados en rojo. A partir de ellos, y sin mirar la gráfica que aparece al principio,
REPRESENTACIÓN DE FUNCIONES Página 5 REFLEXIONA Y RESUELVE Descripción de una gráfica Copia en tu cuaderno los datos encuadrados en rojo. A partir de ellos, y sin mirar la gráfica que aparece al principio,
Volumen de Sólidos de Revolución
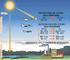
 60 CAPÍTULO 4 Volumen de Sólidos de Revolución 6 Volumen de sólidos de revolución Cuando una región del plano de coordenadas gira alrededor de una recta l, se genera un cuerpo geométrico denominado sólido
60 CAPÍTULO 4 Volumen de Sólidos de Revolución 6 Volumen de sólidos de revolución Cuando una región del plano de coordenadas gira alrededor de una recta l, se genera un cuerpo geométrico denominado sólido
Fundamentos matemáticos. Tema 8 Ecuaciones diferenciales
 Grado en Ingeniería agrícola y del medio rural Tema 8 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2016 Licencia Creative Commons 4.0 Internacional J.
Grado en Ingeniería agrícola y del medio rural Tema 8 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2016 Licencia Creative Commons 4.0 Internacional J.
TEMA 2: DERIVADA DE UNA FUNCIÓN
 TEMA : DERIVADA DE UNA FUNCIÓN Tasa de variación Dada una función y = f(x), se define la tasa de variación en el intervalo [a, a +h] como: f(a + h) f(a) f(a+h) f(a) y se define la tasa de variación media
TEMA : DERIVADA DE UNA FUNCIÓN Tasa de variación Dada una función y = f(x), se define la tasa de variación en el intervalo [a, a +h] como: f(a + h) f(a) f(a+h) f(a) y se define la tasa de variación media
ESTUDIO Y REPRESENTACIÓN GRÁFICA DE FUNCIONES
 ESTUDIO Y REPRESENTACIÓN GRÁFICA DE FUNCIONES 1. Sea f : (0, + ) definida como f () = Ln a) Probar que la función derivada f es decreciente en todo su dominio. b) Determinar los intervalos de crecimiento
ESTUDIO Y REPRESENTACIÓN GRÁFICA DE FUNCIONES 1. Sea f : (0, + ) definida como f () = Ln a) Probar que la función derivada f es decreciente en todo su dominio. b) Determinar los intervalos de crecimiento
Aplicaciones de la derivada Ecuación de la recta tangente
 Aplicaciones de la derivada Ecuación de la recta tangente La pendiente de la recta tangente a una curva en un punto es la derivada de la función en dicho punto. La recta tangente a una curva en un punto
Aplicaciones de la derivada Ecuación de la recta tangente La pendiente de la recta tangente a una curva en un punto es la derivada de la función en dicho punto. La recta tangente a una curva en un punto
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2015 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 05 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 05 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva,
2.1.5 Teoremas sobre derivadas
 si x < 0. f(x) = x si x 0 x o = 0 Teoremas sobre derivadas 9 2. f(x) = x 3, x o = 3 a. Determine si f es continua en x o. b. Halle f +(x o ) y f (x o ). c. Determine si f es derivable en x o. d. Haga la
si x < 0. f(x) = x si x 0 x o = 0 Teoremas sobre derivadas 9 2. f(x) = x 3, x o = 3 a. Determine si f es continua en x o. b. Halle f +(x o ) y f (x o ). c. Determine si f es derivable en x o. d. Haga la
MATEMÁTICAS 2º DE ESO
 MATEMÁTICAS 2º DE ESO LOE TEMA VII: FUNCIONES Y GRÁFICAS Coordenadas cartesianas. Concepto de función. Tabla y ecuación. Representación gráfica de una función. Estudio gráfico de una función. o Continuidad
MATEMÁTICAS 2º DE ESO LOE TEMA VII: FUNCIONES Y GRÁFICAS Coordenadas cartesianas. Concepto de función. Tabla y ecuación. Representación gráfica de una función. Estudio gráfico de una función. o Continuidad
Unidad II. Si una función f(x) tiene primitiva, tiene infinitas primitivas, diferenciándose todas ellas en unaconstante.
 Unidad II Integral indefinida y métodos de integración. 2.1 Definición de integral indefinida. Integrar es el proceso recíproco del de derivar, es decir, dada una función f(x), busca aquellas funciones
Unidad II Integral indefinida y métodos de integración. 2.1 Definición de integral indefinida. Integrar es el proceso recíproco del de derivar, es decir, dada una función f(x), busca aquellas funciones
CARACTERÍSTICAS DE UNA FUNCIÓN
 . DOMINIO CARACTERÍSTICAS DE UNA FUNCIÓN inio de o campo de eistencia de es el conjunto de valores para los que está deinida la unción, es decir, el conjunto de valores que toma la variable independiente.
. DOMINIO CARACTERÍSTICAS DE UNA FUNCIÓN inio de o campo de eistencia de es el conjunto de valores para los que está deinida la unción, es decir, el conjunto de valores que toma la variable independiente.
LA INTEGRAL DEFINIDA Y EL CÁLCULO DE ÁREAS
 LA INTEGRAL DEFINIDA 001. Calcula la integral de f() =, en el intervalo [1, ] 00. Calcula 0 ( + ) d LA INTEGRAL DEFINIDA Y EL CÁLCULO DE ÁREAS 01 ACTIVIDAD PROPUESTA Calcula el área limitada por la función
LA INTEGRAL DEFINIDA 001. Calcula la integral de f() =, en el intervalo [1, ] 00. Calcula 0 ( + ) d LA INTEGRAL DEFINIDA Y EL CÁLCULO DE ÁREAS 01 ACTIVIDAD PROPUESTA Calcula el área limitada por la función
IES Fco Ayala de Granada Septiembre de 2013 (Modelo 3 Especifico) Solucíon Germán-Jesús Rubio Luna. Opción A
 Opción A Ejercicio opción A, modelo 3 Septiembre 03 específico x Sea f la función definida por f(x) = para x > 0, x (donde ln denota el logaritmo neperiano) ln(x) [ 5 puntos] Estudia y determina las asíntotas
Opción A Ejercicio opción A, modelo 3 Septiembre 03 específico x Sea f la función definida por f(x) = para x > 0, x (donde ln denota el logaritmo neperiano) ln(x) [ 5 puntos] Estudia y determina las asíntotas
Matemáticas II PRUEBA DE ACCESO A LA UNIVERSIDAD 2014 BACHILLERATO FORMACIÓN PROFESIONAL CICLOS FORMATIVOS DE GRADO SUPERIOR.
 PRUEBA DE ACCESO A LA UNIVERSIDAD 014 Matemáticas II BACHILLERATO FORMACIÓN PROFESIONAL CICLOS FORMATIVOS DE GRADO SUPERIOR Examen Criterios de Corrección y Calificación UNIBERTSITATERA SARTZEKO PROBAK
PRUEBA DE ACCESO A LA UNIVERSIDAD 014 Matemáticas II BACHILLERATO FORMACIÓN PROFESIONAL CICLOS FORMATIVOS DE GRADO SUPERIOR Examen Criterios de Corrección y Calificación UNIBERTSITATERA SARTZEKO PROBAK
Profesorado de Nivel Medio y Superior en Biología Matemática - 1º Cuatrimestre Año 2013 FUNCIÓN CUADRÁTICA
 Matemática - º Cuatrimestre Año 0 FUNCIÓN CUADRÁTICA Hemos definido anteriormente la función lineal como una función f: R R de la forma f()a+b con a R y b R, que se representa en el plano mediante una
Matemática - º Cuatrimestre Año 0 FUNCIÓN CUADRÁTICA Hemos definido anteriormente la función lineal como una función f: R R de la forma f()a+b con a R y b R, que se representa en el plano mediante una
MATEMÁTICAS BÁSICAS. Autoras: Margarita Ospina Pulido Jeanneth Galeano Peñaloza Edición: Rafael Ballestas Rojano
 MATEMÁTICAS BÁSICAS Autoras: Margarita Ospina Pulido Jeanneth Galeano Peñaloza Edición: Rafael Ballestas Rojano Universidad Nacional de Colombia Departamento de Matemáticas Sede Bogotá Enero de 2015 Universidad
MATEMÁTICAS BÁSICAS Autoras: Margarita Ospina Pulido Jeanneth Galeano Peñaloza Edición: Rafael Ballestas Rojano Universidad Nacional de Colombia Departamento de Matemáticas Sede Bogotá Enero de 2015 Universidad
Grado en Química Bloque 1 Funciones de una variable
 Grado en Química Bloque Funciones de una variable Sección.4: La derivada y sus propiedades básicas. La Regla de la cadena. El concepto de derivada aparece en muchas situaciones en la ciencias: en matemáticas
Grado en Química Bloque Funciones de una variable Sección.4: La derivada y sus propiedades básicas. La Regla de la cadena. El concepto de derivada aparece en muchas situaciones en la ciencias: en matemáticas
1) Considera la función f(x) = x2 + 1 para contestar las siguientes preguntas:
 LIMITE DE FUNCIONES Tema: Introducción a límite 1) Considera la función f(x) = x2 + 1 para contestar las siguientes preguntas: a) Cuál es el valor de la función si x = 2? b) Cuál es el valor de la función
LIMITE DE FUNCIONES Tema: Introducción a límite 1) Considera la función f(x) = x2 + 1 para contestar las siguientes preguntas: a) Cuál es el valor de la función si x = 2? b) Cuál es el valor de la función
No es otra cosa, que la representación de los resultados de una función sobre el plano carteciano.
 FUNCIONES GRAFICAS No es otra cosa, que la representación de los resultados de una función sobre el plano carteciano. INTÉRVALOS Un intervalo es el conjunto de todos los números reales entre dos números
FUNCIONES GRAFICAS No es otra cosa, que la representación de los resultados de una función sobre el plano carteciano. INTÉRVALOS Un intervalo es el conjunto de todos los números reales entre dos números
FUNCIONES REALES DE VARIABLE REAL
 .- Halla el dominio de las siguientes funciones: a) f(x)= x b) x 4 x 3 3x f(x)= + 8x 4 x + 3x 4 x 3 x + 4x c) f(x)= x 3 x x d) 8x 3 + 3x f(x)= 7x x 9 x e) f(x)= x x f) f(x)= x + 5 x g) f(x)= x x + h) f(x)=
.- Halla el dominio de las siguientes funciones: a) f(x)= x b) x 4 x 3 3x f(x)= + 8x 4 x + 3x 4 x 3 x + 4x c) f(x)= x 3 x x d) 8x 3 + 3x f(x)= 7x x 9 x e) f(x)= x x f) f(x)= x + 5 x g) f(x)= x x + h) f(x)=
Matemáticas 2 Agosto 2015
 Laboratorio # 1 Línea recta I.-Determina la ecuación de la recta que satisface las siguientes condiciones y exprésala en la forma general. Pasa por el punto (1,5) y tiene pendiente 2 Pasa por y Pendiente
Laboratorio # 1 Línea recta I.-Determina la ecuación de la recta que satisface las siguientes condiciones y exprésala en la forma general. Pasa por el punto (1,5) y tiene pendiente 2 Pasa por y Pendiente
f: D IR IR x f(x) v. indep. v. dependiente, imagen de x mediante f, y = f(x). A x se le llama antiimagen de y por f, y se denota por x = f -1 (y).
 TEMA 8: FUNCIONES. 8. Función real de variable real. 8. Dominio de una función. 8.3 Características de una función: signo, monotonía, acotación, simetría y periodicidad. 8.4 Operaciones con funciones:
TEMA 8: FUNCIONES. 8. Función real de variable real. 8. Dominio de una función. 8.3 Características de una función: signo, monotonía, acotación, simetría y periodicidad. 8.4 Operaciones con funciones:
CENTRO REGIONAL UNIVERSITARIO BARILOCHE TALLER DE MATEMATICA INGRESO 2016 LIC. ENFERMERÍA PRACTICO UNIDAD 3
 PRACTICO UNIDAD 3 Nota: Los ejercicios propuestos en los prácticos deben servirle para afianzar y practicar temas. Si nota que algunos ejercicios ya los sabe hacer bien, continúe con otros que le impliquen
PRACTICO UNIDAD 3 Nota: Los ejercicios propuestos en los prácticos deben servirle para afianzar y practicar temas. Si nota que algunos ejercicios ya los sabe hacer bien, continúe con otros que le impliquen
Grado en Química Bloque 1 Funciones de una variable
 Grado en Química Bloque Funciones de una variable Sección.5: Aplicaciones de la derivada. Máximos y mínimos (absolutos) de una función. Sea f una función definida en un conjunto I que contiene un punto
Grado en Química Bloque Funciones de una variable Sección.5: Aplicaciones de la derivada. Máximos y mínimos (absolutos) de una función. Sea f una función definida en un conjunto I que contiene un punto
Cálculo diferencial: Concepto y propiedades de una función. Representación gráfica.
 Tema 1 Cálculo diferencial: Concepto y propiedades de una función. Representación gráfica. 1.1. Un esbozo de qué es el Cálculo: paradojas y principales problemas planteados. Los orígenes del Cálculo se
Tema 1 Cálculo diferencial: Concepto y propiedades de una función. Representación gráfica. 1.1. Un esbozo de qué es el Cálculo: paradojas y principales problemas planteados. Los orígenes del Cálculo se
Problemas Tema 1 Solución a problemas de Repaso de 1ºBachillerato - Hoja 02 - Todos resueltos
 página /9 Problemas Tema Solución a problemas de Repaso de ºBachillerato - Hoja 02 - Todos resueltos Hoja 2. Problema. Sea f x )=a x 3 +b x 2 +c x+d un polinomio que cumple f )=0, f ' 0)=2, y tiene dos
página /9 Problemas Tema Solución a problemas de Repaso de ºBachillerato - Hoja 02 - Todos resueltos Hoja 2. Problema. Sea f x )=a x 3 +b x 2 +c x+d un polinomio que cumple f )=0, f ' 0)=2, y tiene dos
Derivadas 6 ACTIVIDADES. 1. Página 140. Función f(x) x 2 1: Función g(x) x 3 7: 2. Página Página Página
 Derivadas 6 ACTIVIDADES 1. Página 140 Función f(x) x 2 1: Función g(x) x 3 7: 2. Página 140 3. Página 141 4. Página 141 5. Página 142 211 Derivadas 6. Página 142 Las derivadas laterales no existen, por
Derivadas 6 ACTIVIDADES 1. Página 140 Función f(x) x 2 1: Función g(x) x 3 7: 2. Página 140 3. Página 141 4. Página 141 5. Página 142 211 Derivadas 6. Página 142 Las derivadas laterales no existen, por
LA INTEGRAL DEFINIDA IES MURILLO
 LA INTEGRAL DEFINIDA IES MURILLO Un poco de Historia El concepto de integral definida surge para resolver el problema del área de figuras limitadas por arcos de curva. Algunos matemáticos que trabajaron
LA INTEGRAL DEFINIDA IES MURILLO Un poco de Historia El concepto de integral definida surge para resolver el problema del área de figuras limitadas por arcos de curva. Algunos matemáticos que trabajaron
La concentración de ozono contaminante, en microgramos por metro cúbico, en una
 ANÁLISIS MATEMÁTICO. PAU CASTILLA Y LEÓN A) EJERCICIOS DE APLICACIÓN A LAS CCSS La concentración de ozono contaminante, en microgramos por metro cúbico, en una ciudad viene dada por la función C ( ) 90
ANÁLISIS MATEMÁTICO. PAU CASTILLA Y LEÓN A) EJERCICIOS DE APLICACIÓN A LAS CCSS La concentración de ozono contaminante, en microgramos por metro cúbico, en una ciudad viene dada por la función C ( ) 90
Universidad de Costa Rica Escuela de Matemática CONARE-PROYECTO RAMA. Funciones
 Universidad de Costa Rica Escuela de Matemática CONARE-PROYECTO RAMA Funciones José R. Jiménez F. Temas de pre-cálculo I ciclo 007 Funciones 1 Índice 1. Funciones 3 1.1. Introducción...................................
Universidad de Costa Rica Escuela de Matemática CONARE-PROYECTO RAMA Funciones José R. Jiménez F. Temas de pre-cálculo I ciclo 007 Funciones 1 Índice 1. Funciones 3 1.1. Introducción...................................
Problemas Tema 4 Solución a problemas de Repaso y Ampliación 1ª Evaluación - Hoja 02 - Problemas 2, 4, 5, 6, 7, 8, 10
 página 1/20 Problemas Tema 4 Solución a problemas de Repaso y Ampliación 1ª Evaluación - Hoja 02 - Problemas 2, 4, 5, 6, 7, 8, 10 Hoja 2. Problema 2 Resuelto por Carmen Jiménez Cejudo (diciembre 2014)
página 1/20 Problemas Tema 4 Solución a problemas de Repaso y Ampliación 1ª Evaluación - Hoja 02 - Problemas 2, 4, 5, 6, 7, 8, 10 Hoja 2. Problema 2 Resuelto por Carmen Jiménez Cejudo (diciembre 2014)
FUNCIONES CUADRÁTICAS
 FUNCIONES CUADRÁTICAS A la función polinómica de segundo grado f(x) = ax 2 + bx + c, siendo a, b, c, números reales y a 0 se la denomina función cuadrática. Dominio de una función cuadrática es el conjunto
FUNCIONES CUADRÁTICAS A la función polinómica de segundo grado f(x) = ax 2 + bx + c, siendo a, b, c, números reales y a 0 se la denomina función cuadrática. Dominio de una función cuadrática es el conjunto
IES Fco Ayala de Granada Modelos del 2010 (Modelo 1) Soluciones Germán-Jesús Rubio Luna. Opción A
 Opción A Ejercicio opción A, modelo de año 200 [2 5 puntos] Entre todos los triángulos rectángulos de 5 metros de hipotenusa, determina los catetos del de área máxima. Función a maximizar A (/2)(x)(y)
Opción A Ejercicio opción A, modelo de año 200 [2 5 puntos] Entre todos los triángulos rectángulos de 5 metros de hipotenusa, determina los catetos del de área máxima. Función a maximizar A (/2)(x)(y)
Modelo1_2009_Enunciados. Opción A
 a) Duración: hora y 30 minutos. b) Tienes que elegir entre realizar únicamente los cuatro ejercicios de la o realizar únicamente los cuatro ejercicios de la. e) Se permitirá el uso de calculadoras que
a) Duración: hora y 30 minutos. b) Tienes que elegir entre realizar únicamente los cuatro ejercicios de la o realizar únicamente los cuatro ejercicios de la. e) Se permitirá el uso de calculadoras que
14.1 Introducción. 14.2 Caso 1: Area bajo una curva.
 Temas. Capacidades Calcular áreas de regiones del plano. 14.1 Introducción Area bajo una curva En esta sesión se inicia una revisión de las principales aplicaciones de la integral definida. La primera
Temas. Capacidades Calcular áreas de regiones del plano. 14.1 Introducción Area bajo una curva En esta sesión se inicia una revisión de las principales aplicaciones de la integral definida. La primera
Capítulo 4: Derivada de una función
 Capítulo 4: Derivada de una función Geovany Sanabria Contenido Razones de cambio 57 Definición de derivada 59 3 Cálculo de derivadas 64 3. Propiedadesdederivadas... 64 3.. Ejercicios... 68 3. Derivadasdefuncionestrigonométricas...
Capítulo 4: Derivada de una función Geovany Sanabria Contenido Razones de cambio 57 Definición de derivada 59 3 Cálculo de derivadas 64 3. Propiedadesdederivadas... 64 3.. Ejercicios... 68 3. Derivadasdefuncionestrigonométricas...
DE LA GRÁFICA A LA EXPRESIÓN ALGEBRAICA
 De la gráfica a la expresión algebraica DE LA GRÁFICA A LA EXPRESIÓN ALGEBRAICA Rectas, Parábolas, Hipérbolas, Exponenciales Logarítmicas LA RECTA Comencemos localizando el punto donde la recta corta al
De la gráfica a la expresión algebraica DE LA GRÁFICA A LA EXPRESIÓN ALGEBRAICA Rectas, Parábolas, Hipérbolas, Exponenciales Logarítmicas LA RECTA Comencemos localizando el punto donde la recta corta al
